A long-standing goal in computational chemistry is to combine the quantum description of nonadiabatic processes with the simple classical trajectories in molecular dynamics (MD). In classical MD one calculates molecular properties via an average over many particles that follow Newtonian mechanics on a potential energy surface, which emerges from the famous Born-Oppenheimer approximation. This approximation is however no longer valid for nonadiabatic processes, such as interaction with light, internal conversion and ultrafast electron transfer. To describe these phenomena one has to include multiple potential energy surfaces, which raises the question: is it possible to combine classical MD trajectories with nonadiabatic dynamics on multiple surfaces in a rigorous way?

In my talk I will show a simple way to achieve this for a two-surface problem, without invoking the surface-hopping ansatz. The key idea is to assign an additional pair of variables to each trajectory to describe the electronic states, in addition to the nuclear coordinates and momenta. These variables are encoded as the orientation of a unit vector on a sphere, where the north pole represents the ground state, the south pole represents the excited state, and other points on the sphere represent general superpositions of both surfaces. We have showed[1] how to derive a mixed quantum-classical method in this way, which shares the same equations of motion as in Ehrenfest dynamics, but differs in an important way in how initial distributions and observables are defined.

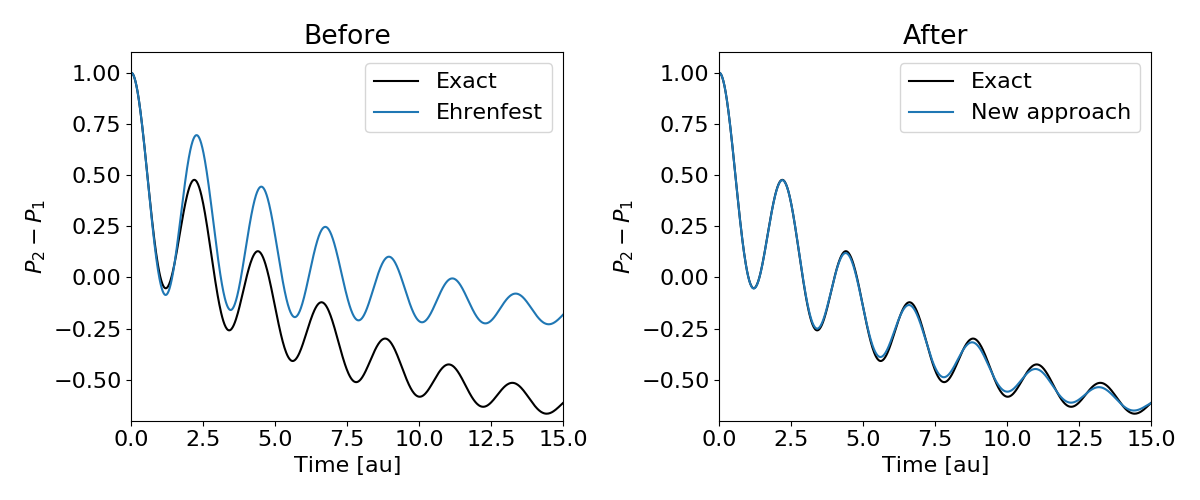
I will show benchmark results for the approach applied to population transfer in various model systems. The figure shows an example of the population difference between two electronic states for a condensed-phase system that is initially in its excited state. Ehrenfest dynamics predicts completely wrong final state populations, whereas our method is in almost perfect agreement with the exact result.

[1] J. E. Runeson and J. O. Richardson. arXiv:1904.08293 [physics.chem-ph] (2019).